The brachistochrone curve: the problem of quickest descent

Suppose there is an incline such as that shown below.
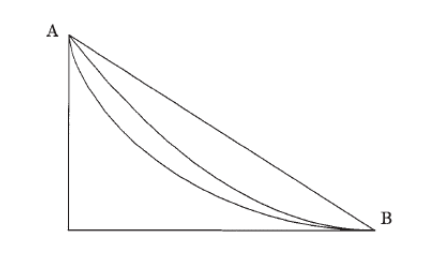
When a ball rolls from A to B, which curve yields the shortest duration? Let’s assume that we have three hypotheses: a straight line, a quadratic, and a cycloid. The shortest path from A to B is the straight line, so one might think that the straight path is the fastest, but in fact it is surprisingly slow. It’s better to select a path which has a downward drop in order to accelerate the ball in the first phase, so that it rolls quickly. The ball arrives earlier on the quadratic path than on the straight line path. However, increasing the degree of the function causes the ball to travel more slowly on the flat section.
It is said that Galileo (1564-1642) first presented this problem. It is also known that the cycloid is the curve which yields the quickest descent. This time I will discuss this problem, which may be handled under the field known as the calculus of variations, or variational calculus in physics, and introduce the charming nature of cycloid curves. (...)
I explained that the cycloid was the curve of quickest descent, but it has one more exceptional property, it is isochronic. Whether a ball is rolled from the point A shown in Figure 4, or from the intermediate point C, the time taken to arrive at point B is the same. (...)
The cycloid pendulum devised by Huygens is the same as Figure 5 flipped vertically with the central half removed (Figure 6). With this pendulum, even when the swing is large, isochronism is maintained. Clocks employing this principle are more accurate than Galileo clocks. (...)
Nowadays actual models of the Brachistochrone curve can be seen only in science museums. But we should not forget that the problem of quickest descent mathematically developed the study of the cycloid and the calculus of variations, and contributed to the improvement of pendulums.
PS: you can find brachistochrones in snowboard half-pipes ;)
http://www.iitgn.ac.in/mcm/cd/mcm-2011/PDFs/Problem_A/11199.pdf
